前前后后看了一个星期的关于optimization programmer 和cache 方面的知识,虽然没有打开课本,但想直接做做,课本属实有点厚,主要是想快刀斩乱麻

太难啦!!!!

预备知识

Rules and Tips

WriteUp，本lab的规则与评分标准。
书本内容及实验，这个ppt其实非常好，回顾了书本上的内容，对实验部分也给予了一定的引导作用。
分块技术，CMU早年的一篇文章，配合Lab食用体验更佳。

小函数

getopt用法,能在给定的命令参数中挑出选项,识别不同种类的参数
fscanf用法,能在包含大量相同格式的文件中,分别读出每一个字符

函数原型：

1	Copyint fscanf(FILE * fp,char * format,...);

其中fp为文件指针，format为C字符串，…为参数列表，返回值为成功写入的字符的个数。

fscanf函数会从文件输入流中读入数据，存储到format中，遇到空格和换行时结束。

例如本文

1	fscanf(fp, "%c %xu,%d\n", &operation, &address, &size

能从fp对应的文件中每一行读取一个字符存到operation,读取一个16进制无符号整数存到Address,读取一个整数存到Size

malloc用法,能开辟空间

函数声明

1	void *malloc(size_t size)

返回值:

该函数返回一个指针,指向已分配大小的内存。如果请求失败,则返回NULL。

例如本文:

1	cache_ = (cache)malloc(sizeof(cache_f) * S);

返回的指针无类型,需要自己规定类型.

fopen用法: 定位文件(通过路径),以指针的形式访问文件

函数声明

1	FILE fopen(const char filename, const char *mode)

例如本文

FILE *fp = NULL;
    fp = fopen(t, "r");
    if (fp == NULL)
    {
        printf("Fuck you Open error!!!");
        exit(-1);
    }

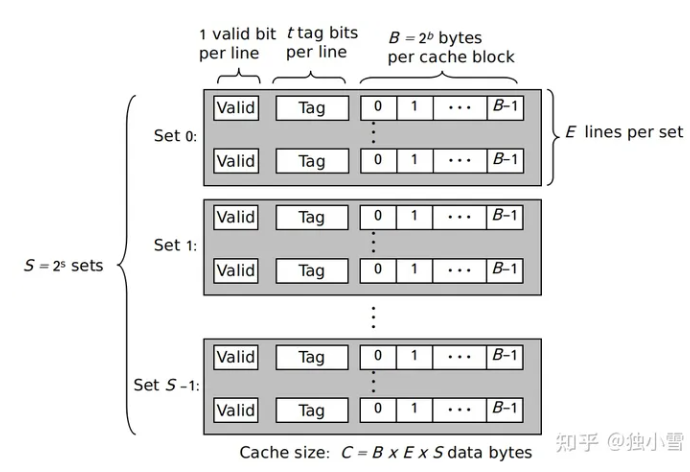
Cache寻址

缓存长什么样?

故缓存中的每个Cache_line由Valid_bits和Tag和Block构成,每个Set由有多个E,每个E有多个line.具体可以看视频,要是看不懂的话,可以看课程视频.

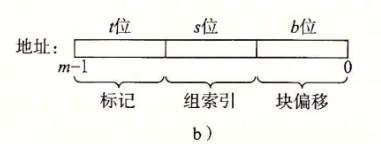
相信你现在懂了,那我们再看看怎么寻址吧!

每一个内存对缓存的映射大都符合这种情况,有一个tag,有一个set index,有一个Block offset.了解了解就可以开始做题了!

希望上面的每个链接你都能细致的看完,不然的话就要像我一样没有完备的知识架构体系而不断的上网查资料了,这就是精华!!!

Part 1 LRU Cache

目的:在给定的csim.c文件中编写填充,实现一个基于LRU策略的Cache simulator,该模拟器可以模拟在一系列的数据访问中cache的hit、miss与eviction的情况，其中，需要eviction行时，用LRU替换策略进行替换。

cache模拟器需要能处理一系列如下的命令：

Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile>

其中各参数意义如下：

-h：输出帮助信息的选项；
-v：输出详细运行过程信息的选项；
-s：组索引的位数(意味着组数S=2^s^)；
-E：每一组包含的行数；
-b：偏移位的宽度(意味着块的大小为B=2^b^);
-t：输入数据文件的路径(测试数据从该文件里面读取)。

———————————————

接下来分别讲解每个函数的思路和代码实现:

sf

在这个函数里面我要做的是把输入的,在命令行中的参数全部提取出来,这里采取的是getopt函数(注意加上他的头文件),要是你学会了他的用法那就不难了,opt会依次获取每一个选项h,v,s,E,b,t要是有就会读入,要是有冒号的话还会读入后面的参数,存在optarg中,通过atoi函数可以直接将字符串转换成整数!完美解决第一个小函数

void sf(int argc,char ** argv){
    h = 0;
    v = 0;
    int opt;
    // 拆分输入的规定
    while (-1 != (opt = (getopt(argc, argv, "hvs:E:b:t:"))))
    {
        switch (opt)
        {
            case 'h':
                h = 1;
                printUsage();
                break;
            case 'v':
                v = 1;
                printUsage();
                break;
            case 's':
                s = atoi(optarg);
                break;
            case 'E':
                E = atoi(optarg);
                break;
            case 'b':
                b = atoi(optarg);
                break;
            case 't':
                strcpy(t, optarg);
                break;
            default:
                printUsage();
                break;
        }
    }
    if (s <= 0 || E <= 0 || b <= 0 || t == NULL)
        exit(-1);
    S = 1 << s;
}

PrintUsage

这个函数可要可不要,我随便写的

void printUsage()
{
    printf("Fuck you Vite ,Do it quickly ,Don't play game! OK?\n"
           "Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n"
           "Options:\n"
           "  -h         Print this help message.\n"
           "  -v         Optional verbose flag.\n"
           "  -s <num>   Number of set index bits.\n"
           "  -E <num>   Number of lines per set.\n"
           "  -b <num>   Number of block offset bits.\n"
           "  -t <file>  Trace file.\n\n"
           "Examples:\n"
           "  linux>  ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n"
           "  linux>  ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n");
}

init_Cache

接下来,开始给Cache分配空间,我们要使用lru策略,所以每一个cache的组成部分都要有valid_bits和tag和stamp(时间戳),三部分构成,考虑到其就像一个二维数组,故我们用一个结构体二维数组来模拟

先创建结构体,同时创建了一级指针和二级指针

typedef struct
{
    int valid_bits;
    int tag;
    int stamp;
} cache_line, *cache_f, **cache;
cache cache_ = NULL;

然后开始初始化结构体

先给一级指针开辟空间,再分别给每一个结构体开辟空间,以访问数组的方式初始化每个struct内的三个小玩意,便算是整个初始化完毕了.

void init_cache()
{
    cache_ = (cache)malloc(sizeof(cache_f) * S);
    for (int i = 0; i < S; i++)
    {
        cache_[i] = (cache_f)malloc(sizeof(cache_line) * E);
        for (int j = 0; j < E; j++)
        {
            cache_[i][j].valid_bits = 0;
            cache_[i][j].tag = -1;
            cache_[i][j].stamp = -1;
        }
    }
}

simulate_cache

模拟cache,首先检验我们得到的t路径能不能用,若fp是一个空指针,则该文件不存在,输出错误信息.然后就要通过while循环和fscanf函数来读取给定的trace文件夹中的指令

显然,里面的指令都是一个operation+address+size,由给定的write up中说到,不用统计I这个指令,所以我们只用考虑Load,Store和Modify三个指令,Modify可以理解为L+S,所以我们通过fscanf得到指令选项后,’L’,’S’都只要更新一次,’M’要更新两次,同时每次读取文件的其中一行我们都要模拟缓存的LRU策略,更新时间戳.

void simulate_cache()
{
    FILE *fp = NULL;
    fp = fopen(t, "r");
    if (fp == NULL)
    {
        printf("Fuck you Open error!!!");
        exit(-1);
    }
    char operation;
    unsigned int address;
    int size;
    while (fscanf(fp, "%c %xu,%d\n", &operation, &address, &size) > 0)
    {
        switch (operation)
        {
        case 'L':
            update(address);
            break;
        case 'M':
            update(address);
        case 'S':
            update(address);
            break;
        }
        update_stamp();
    }
    fclose(fp);
    for (int i = 0; i < S; i++)
        free(cache_[i]);
    free(cache_);
}

当然在遍历完trace文件后,我们要记得关闭文件夹指针,同时挨个挨个释放malloc分配的空间.毕竟有借有还,再借不难!

update

这里我们这样模拟:对于传进来的地址,我们先要拆出他的set_index,拆出他的tag,Block Offset的位数由给定的-b参数决定,set_index由-s的参数决定,故我们通过进制位移得到如下:

1 2	unsigned set_address = ((address >> b) & ((-1U) >> (64 - s))); int cache_tag = address >> (s + b);

然后我们取到了这几个地址后就要分别判断是hit,还是miss,还是miss+eviction,所以我们要分别判断在对应的set里面,遍历一次.

第一个循环判断的是能否hit
第二个循环判断的是是否有空行能够使用
第三个循环把使用时间最久的行驱逐换上新的行,复位时间戳.

void update(unsigned int address)
{
    unsigned set_address = ((address >> b) & ((-1U) >> (64 - s)));
    int cache_tag = address >> (s + b);
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].tag == cache_tag)
        {
            hit_count++;
            cache_[set_address][i].stamp = -1;
            return;
        }
    }
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].valid_bits == 0)
        {
            miss_count++;
            cache_[set_address][i].valid_bits = 1;
            cache_[set_address][i].stamp = 0;
            cache_[set_address][i].tag = cache_tag;
            return;
        }
    }
    int max_stamp = -1;
    int waste = -1;
    miss_count++;
    eviction_count++;
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].stamp > max_stamp)
        {
            max_stamp = cache_[set_address][i].stamp;
            waste = i;
        }
    }
    cache_[set_address][waste].stamp = 0;
    cache_[set_address][waste].tag = cache_tag;
}

update_stamp

更新时间戳很简单,就是把合法情况全遍历一遍,时间戳都加一

void update_stamp()
{
    for (int i = 0; i < S; i++)
    {
        for (int j = 0; j < E; j++)
            if (cache_[i][j].valid_bits == 1)
                ++cache_[i][j].stamp;
    }
}

总体代码:

#include "cachelab.h"
#include <stdlib.h>
#include <unistd.h>
#include <getopt.h>
#include <string.h>
#include <stdio.h>
int h, v, s, E, b, S;
int hit_count, miss_count, eviction_count;
char t[1000];
typedef struct
{
    int valid_bits;
    int tag;
    int stamp;
} cache_line, *cache_f, **cache;
cache cache_ = NULL;
void printUsage()
{
    printf("Fuck you Vite ,Do it quickly ,Don't play game! OK?\n"
           "Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n"
           "Options:\n"
           "  -h         Print this help message.\n"
           "  -v         Optional verbose flag.\n"
           "  -s <num>   Number of set index bits.\n"
           "  -E <num>   Number of lines per set.\n"
           "  -b <num>   Number of block offset bits.\n"
           "  -t <file>  Trace file.\n\n"
           "Examples:\n"
           "  linux>  ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n"
           "  linux>  ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n");
}

void init_cache()
{
    cache_ = (cache)malloc(sizeof(cache_f) * S);
    for (int i = 0; i < S; i++)
    {
        cache_[i] = (cache_f)malloc(sizeof(cache_line) * E);
        for (int j = 0; j < E; j++)
        {
            cache_[i][j].valid_bits = 0;
            cache_[i][j].tag = -1;
            cache_[i][j].stamp = -1;
        }
    }
}
void update(unsigned int address)
{
    unsigned set_address = ((address >> b) & ((-1U) >> (64 - s)));
    int cache_tag = address >> (s + b);
    //
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].tag == cache_tag)
        {
            hit_count++;
            cache_[set_address][i].stamp = -1;
            return;
        }
    }
    //
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].valid_bits == 0)
        {
            miss_count++;
            cache_[set_address][i].valid_bits = 1;
            cache_[set_address][i].stamp = 0;
            cache_[set_address][i].tag = cache_tag;
            return;
        }
    }
    //
    int max_stamp = -1;
    int waste = -1;
    miss_count++;
    eviction_count++;
    for (int i = 0; i < E; i++)
    {
        if (cache_[set_address][i].stamp > max_stamp)
        {
            max_stamp = cache_[set_address][i].stamp;
            waste = i;
        }
    }
    cache_[set_address][waste].stamp = 0;
    cache_[set_address][waste].tag = cache_tag;
}
void update_stamp()
{
    for (int i = 0; i < S; i++)
    {
        for (int j = 0; j < E; j++)
            if (cache_[i][j].valid_bits == 1)
                ++cache_[i][j].stamp;
    }
}
void simulate_cache()
{
    FILE *fp = NULL;
    fp = fopen(t, "r");
    if (fp == NULL)
    {
        printf("Fuck you Open error!!!");
        exit(-1);
    }
    char operation;
    unsigned int address;
    int size;
    while (fscanf(fp, "%c %xu,%d\n", &operation, &address, &size) > 0)
    {
        switch (operation)
        {
        case 'L':
            update(address);
            break;
        case 'M':
            update(address);
        case 'S':
            update(address);
            break;
        }
        update_stamp();
    }
    fclose(fp);
    for (int i = 0; i < S; i++)
        free(cache_[i]);
    free(cache_);
}
void sf(int argc,char ** argv){
    h = 0;
    v = 0;
    int opt;
    // 拆分输入的规定
    while (-1 != (opt = (getopt(argc, argv, "hvs:E:b:t:"))))
    {
        switch (opt)
        {
        case 'h':
            h = 1;
            printUsage();
            break;
        case 'v':
            v = 1;
            printUsage();
            break;
        case 's':
            s = atoi(optarg);
            break;
        case 'E':
            E = atoi(optarg);
            break;
        case 'b':
            b = atoi(optarg);
            break;
        case 't':
            strcpy(t, optarg);
            break;
        default:
            printUsage();
            break;
        }
    }
    if (s <= 0 || E <= 0 || b <= 0 || t == NULL)
        exit(-1);
    S = 1 << s;
}
int main(int argc, char **argv)
{
    sf (argc,argv);
    init_cache();
    simulate_cache();
    printSummary(hit_count, miss_count, eviction_count);
}

Part_2 Block

注意事项

限制条件

给定的是s=5,E=1,b=5;故S=1<<s ==> S=32

故一共有32组set,每组1line,每line有32Bytes,由tran.c内的函数可知,矩阵中存的是int类型的数组故每个cache_line能存8个int 变量

Rules

• Your code in trans.c must compile without warnings to receive credit.

• You are allowed to deﬁne at most 12 local variables of type int per transpose function.1

• You are not allowed to side-step the previous rule by using any variables of type long or by using any bit tricks to store more than one value to a single variable.

• Your transpose function may not use recursion.

• If you choose to use helper functions, you may not have more than 12 local variables on the stack at a time between your helper functions and your top level transpose function. For example, if your transpose declares 8 variables, and then you call a function which uses 4 variables, which calls another function which uses 2, you will have 14 variables on the stack, and you will be in violation of the rule.

• Your transpose function may not modify array A. You may, however, do whatever you want with the contents of array B.

• You are NOT allowed to deﬁne any arrays in your code or to use any variant of malloc.

Eg:4*4

因为题目条件,一个set只有一个line,一个line里面只有一个block,所以我们说的line和block在part_2里面几乎可以划为等价符号.

以4*4分块为例子分析,以文章的限定条件,一个cache_line能存放8个int类型的数据,我们同样知道要是存到缓存中A的第一二行都会在同一个line里面而三四行在第二个line里面.

我们分别用朴素代码跑一遍

# 朴素代码
void trans(int M, int N, int A[N][M], int B[M][N]){
    int i, j, tmp;
    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    }    
}

我们测试一下原始代码

1	make && ./test-trans -M 4 -N 4

结果如下

1	hits:15, misses:22, evictions:19

重点分析原始代码,即自带的朴素转置造成多miss的原因

我们在终端输入以下命令来跟踪输出(命令能在文首的write up链接的pdf中看见,请仔细看!!!)

1	./csim-ref -v -s 5 -E 1 -b 5 -t f(i) > trace(i).txt//f(i)为函数顺序输出的文件 fi要看你是第几个函数,会输出对应的fi(1,2,3,4...)的跟踪文件,然后用csim-ref模拟跑一遍

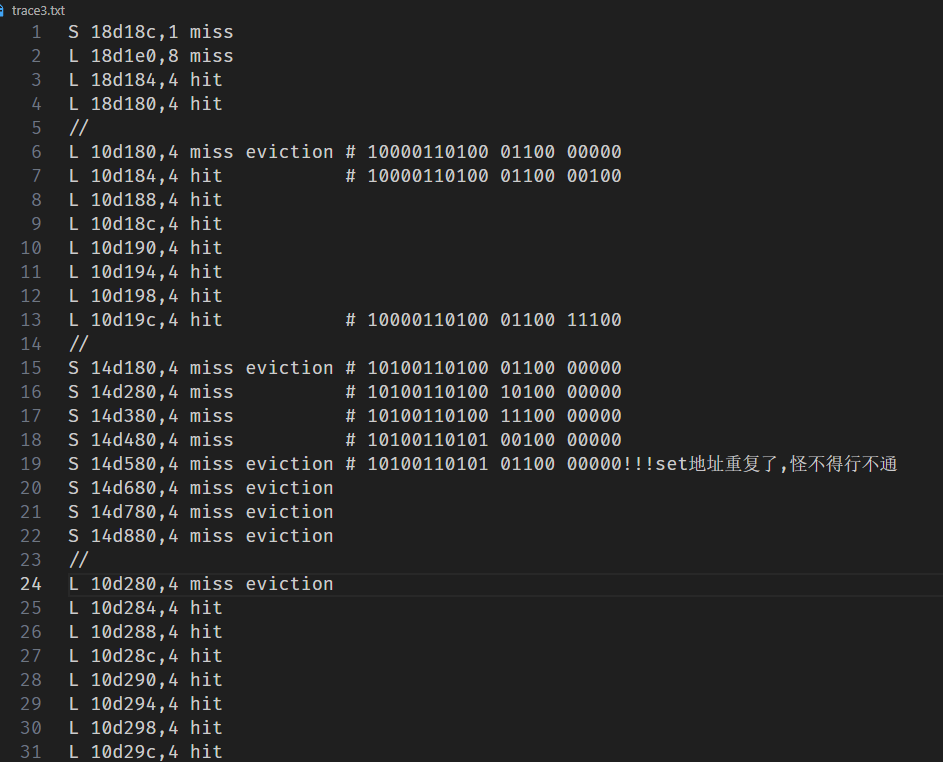
这个是朴素代码的跟踪结果,我们观察分析

S 18d0cc,1 miss 
L 18d100,8 miss 
L 18d0c4,4 hit 
L 18d0c0,4 hit   
//Valgrind 模拟,函数,等等的系统性开支
-------
L 10d0c0,4 miss eviction  A数组访问A[0][0]，冷不命中，将块11装入cache
S 14d0c0,4 miss eviction  虽然B[0][0]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache
L 10d0c4,4 miss eviction  A数组访问A[0][1]，虽然A[0][1] 所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。
S 14d0d0,4 miss eviction  虽然B[1][0]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache
L 10d0c8,4 miss eviction  虽然A[0][2]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。

S 14d0e0,4 miss               B数组访问B[2][0]，B[2][0] 所映射的块12不在cache中，冷不命中，将数组B对应的块12装入cache
L 10d0cc,4 hit                   A[0][3]所映射的块11在cache中，且标记位相同，故命中。
S 14d0f0,4 hit                   Bhit
L 10d0d0,4 hit                  A[1][0]所映射的块11在cache中，且标记位相同，故命中。
S 14d0c4,4 miss eviction  虽然B[0][1] 所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache。
......

我们能发现,他之所以冲突就是因为在朴素代码中,由于A,B两个数组下标相同时,或者是因为其在缓存上的排列,当两个块在缓存中的映射位置相同时,例如A[0,0]已经加载到缓存中了,为了个B[0,0]赋值,只能把A[0,0]驱逐,但是写完B[0,0]后又要读入A[1,0],其映射的块又是在11(这个是由地址算出来的),所以B[0,0]又要被驱逐,重复很多次的冲突所以就会导致miss数量维持较高.

所以我们有什么办法呢?我们知道:
要先读入A数组再读入B数组,有没有办法能一次性读完A进入到缓存的部分呢?有的!,由上图我们知道A进入缓存的部分11块中有8个int,所以我们可以创建8个局部变量,把这8个int都存起来,然后再把b读进来,这样读过的A就不用再读了!就可以减少很多冲突!

代码如下:

#优化代码
void trans_test(int M,int N,int A[N][N],int B[N][N]){
    int x1,x2,x3,x4,x5,x6,x7,x8,i;
for( i=0;i<3;i+=2){
     x1=A[i][0],x2=A[i][1],x3=A[i][2], x4=A[i][3],x5=A[i+1][0],x6=A[i+1][1],x7=A[i+1][2], x8=A[i+1][3];
     B[0][i]=x1;,B[1][i]=x2,B[2][i]=x3, B[3][i]=x4,B[0][i+1]=x5,B[1][i+1]=x6,B[2][i+1]=x7,B[3][i+1]=x8;
}
}

测试结果如下:

1	hits:29, misses:8, evictions:5

miss数大量减少,所以要是可以理解的话,我们就继续往下看趴!

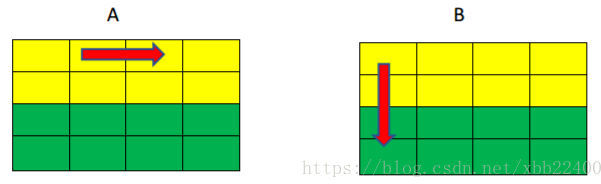
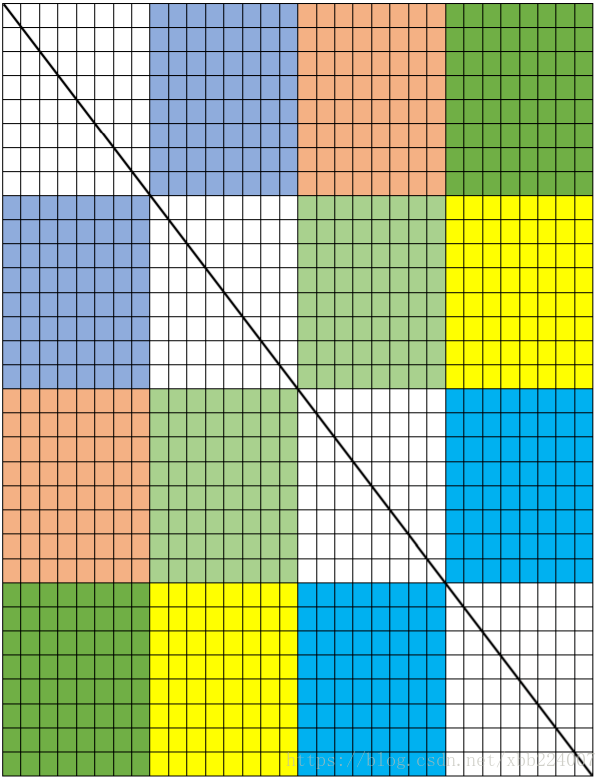
Phase_1:32*32

通关思路

依据ppt的内容,我们往分块方向上去讨论,8*8分块,因为一个cache_line只能存8个int,所以我们使用8*8的分块形式能恰好利用到前八行由下面的图可以看出,除却对角线上的元素,对应色块的转置采用8*8几乎是互不干扰的,因为其映射的地址不一样,所以我们将cache划分成从上往下共四份是有用的.所以我们在每个分块里单独进行转置,能减少很多次因为冲突而导致的Miss.

char trans_1_desc[]="直接进行8*8的分块,不做任何优化";
void trans_1(int M,int N,int A[N][N],int B[N][N]){
    if(M==32){
        for(int i=0;i<M;i+=8)
        for(int j=0;j<N;j+=8)
        for(int m=i;m<8+i;m++)
        for(int n=j;n<8+j;n++)
        B[n][m]=A[m][n];
    }
}

然后便会得到以下结果

对角线图示:

Miss:343离满分差了一点,我们发现色块之间的转置其实已经优化到上限了,现在要优化的就是对角线,因为对角线上的快存在原地转置的问题,比如A[0,0]和B[0,0]对应的位置其实是一样的,在这里面要是不特殊操作那发生的情况就类似于4*4的情况.要是你对4*4的例子理解透彻的话,那很简单,我们只用把A一整行的8个int全部都取出来,存在8个局部变量中,再转置到b,这样就能大大简化eviction的数量了.

优化一下对角线代码,即对内层进行展开.

char trans_2_desc[]="进行8*8的分块,并且优化对角线";
void trans_2(int M,int N ,int A[M][N],int B[M][N])
{int i,j,m,n,x1,x2,x3,x4,x5,x6,x7,x8;
    for( i=0;i<M;i+=8){
        for( j=0;j<N;j+=8){
            if(i==j){
                for(m=i;m<8+i;m++)
                {
                   x1=A[m][j];
                   x2=A[m][j+1];
                   x3=A[m][j+2];
                   x4=A[m][j+3];
                   x5=A[m][j+4];
                   x6=A[m][j+5];
                   x7=A[m][j+6];
                   x8=A[m][j+7];
                   B[j][m]=x1;
                   B[j+1][m]=x2;
                   B[j+2][m]=x3;
                   B[j+3][m]=x4;
                   B[j+4][m]=x5;
                   B[j+5][m]=x6;
                   B[j+6][m]=x7;
                   B[j+7][m]=x8;               
                }   
            }
             else {
                    for( m=i;m<8+i;m++)
                    for( n=j;n<8+j;n++)
                    B[n][m]=A[m][n];
                }
        }
    }
}

Miss数为287个,达到满分标准

最简优化思路

但是理论值256?(32*4*2=256不包括Valgrind模拟产生的开销),可以考虑再优化.

我们想想,还有哪里会消耗呢?色块已经到上限了,那还是继续考虑对角线上的块.我们考虑到,每次我们都是这样做的,模拟下流程:

Load A[1]

Load B[1-8]—>evict A[1]

Load A[2] —>evict B[2]

Load B[2] —>evict A[2]

…

Load A[7] —>evict B[7]

Load B[7] —>evict A[7]

Load A[8] —>evict B[8]

Load B[8] —>evict A[8]

有没有什么办法可以减少evict的次数呢?有两种可能

Load A[i] 前 Load B[i]
Load B[i] 前 Load A[i]

第一种pass,毕竟a是原数组,所以有没有办法把A[i]的值先放起来,再之后再Load对应的B[i]呢,我们发现,A的每一行只会load一遍,所以啊我们只用把A的那一行都用寄存器存起来后再把B对应的那一行load进去,相当于一行一行的把A复制到B中,最后所有的B都加载到缓存中了,再借助一个中间变量转置就好了,简单易懂!

char trans_3_desc[]="进行8*8的分块,并且优化对角线,逼近极限";
void trans_3(int M,int N ,int A[M][N],int B[M][N]){
int i,j,m,n,x1,x2,x3,x4,x5,x6,x7,x8;
    for( i=0;i<M;i+=8){
        for( j=0;j<N;j+=8){
            if(i==j){
                for(m=i;m<8+i;m++){
                    x1=A[m][j],x2=A[m][j+1],x3=A[m][j+2],x4=A[m][j+3],x5=A[m][j+4],x6=A[m][j+5],x7=A[m][j+6],x8=A[m][j+7];
                    B[m][j]=x1,B[m][j+1]=x2,B[m][j+2]=x3,B[m][j+3]=x4,B[m][j+4]=x5,B[m][j+5]=x6,B[m][j+6]=x7,B[m][j+7]=x8;
                }//复制
                for(m=i;m<8+i;m++){
                    for(n=j;n<j+8;n++)
                    if(m+1<=n){
                    x1=B[m][n];
                    B[m][n]=B[n][m];
                    B[n][m]=x1;
                    }           //原地转置
                }
            }
             else {
                    for( m=i;m<8+i;m++)
                    for( n=j;n<8+j;n++)
                    B[n][m]=A[m][n];
                }
        }
    }
}

测试结果如下:

1	hits:2242, misses:259, evictions:227

Phase_2:64*64

正常解法

矩阵长宽各变成32*32的一倍,那简单,我们直接把之前做的矩阵优化丢进去一测试,完蛋!

1 2	func 0 (Simple row-wise scan transpose): hits:3474, misses:4723, evictions:4691 func 2 (进行8*8的分块,并且优化对角线): hits:3586, misses:4611, evictions:4579

相较于给定的朴素函数竟然只有这么点提升,怎么回事呢?我们直接将把路径跟踪一下,不得了

怎么会有这么多个miss eviction呢?一看地址,发现A load是没问题的,但是B Store就出现了问题,每次的后四个块地址就映射到前四个块的地址了,这小陷阱竟然被我发现了(逃,所以我们初步想一想是不是该进行8*4的分块来进行操作呢,说办就办

char trans_4_desc[]="64*64的矩阵,思考分块8*4";
void trans_4(int M,int N,int A[M][N],int B[M][N]){
    int i,j,m,n;
    for( i=0;i<M;i+=8)
    for( j=0;j<N;j+=4)
    for(m=i;m<i+8;m++)
    for(n=j;n<j+4;n++)
    B[m][n]=A[n][m];
}

很快的得到了miss为

1	hits:6354, misses:1843, evictions:1811

那是不是还要再优化一下对角线呢?这不太好优化,先想想满分是1300miss,我们采取8*4的块,这样子有点抽象,存在后四位数字用不到的情况,所以我们采取4*4试一试

char trans_5_desc[]="64*64的矩阵,思考分块4*4";
void trans_5(int M,int N,int A[M][N],int B[M][N]){
    int i,j,x,x1,x2,x3,x4;
    for( i=0;i<M;i+=4)
    for( j=0;j<N;j+=4)
    for(x=i;x<i+4;x++)
    {
        x1=A[x][j],x2=A[x][j+1],x3=A[x][j+2],x4=A[x][j+3];
        B[j][x]=x1,B[j+1][x]=x2,B[j+2][x]=x3,B[j+3][x]=x4;
    }
}

可以得到以下结果

1	hits:6498, misses:1699, evictions:1667

1699miss,看来想单纯考分块是不能过关的,所以只好继续思考8*4分块的优化方式,因为采取4*4分块的话,每一次Load A 在8*4分块中只需要一次,但在4*4中要两次,44分块的不足之处还是太严重了,所以只能继续思考8*4的分块方式,看能不能想象办法优化一下.

再想一想B的Store的顺序分别为:

前四行前四列–>后四行前四列—>前四行后四列—>后四行后四列,所以得想个办法让B先不跳转到后四行,👍

在这里要引用这个链接,他讲的真心不错,图文并茂.

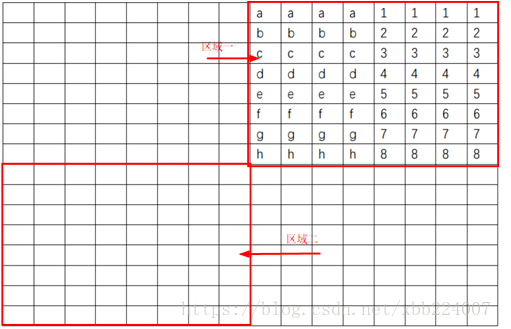
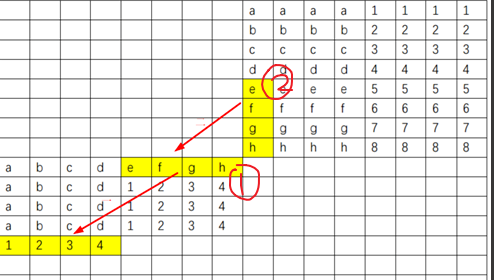
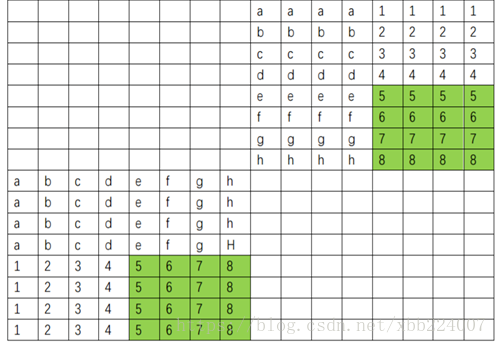
这是我们要转置的区域,虽然我们想8*4的转置,但还是建立在8*8的区域上面去转置的,画图真的能帮助分析理解,为了尽量减少冲突造成的miss,毕竟考虑到对角线的各种映射冲突导致的miss,我们尽量在读完一行后不再读它,所以每次用8个x来最大可能地保存值,从而让miss数尽可能的低

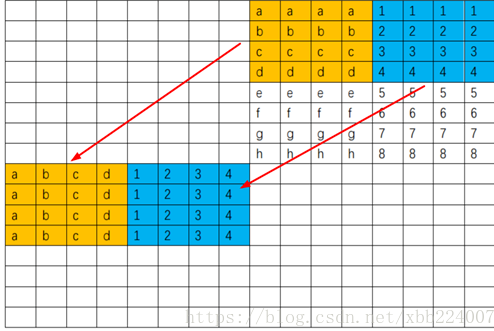
所以为了不再访问前四行,我们把那些元素都取出来,顺便把元素提前转置了,之后直接平移就可以了

有八个局部变量,所以我们先把{1}位置四个值存起来,然后把{2}位置的值丢进去,然后就可以不读这一行了,读第五行然后把存下来的关于{1}的值平移下去,重复四遍这种行为就好了.

最后再转置后四行的后四列,这就是常规转置了,合理利用8个局部变量.

当然我们在这里还是可以考虑对角线原地转置导致的miss,但对于一个8*4的块来说还是比较复杂的,等我以后牛逼了再来讨论(2024.3.12)

char trans_6_desc[]="64*64的矩阵,思考分块8*8下以8*4为小块进行转置";
void trans_6(int M,int N,int A[M][N],int B[M][N]){
        int i,j,x,y,x1,x2,x3,x4,x5,x6,x7,x8;
        for( i=0;i<M;i+=8){
            for( j=0;j<N;j+=8){
                //开始讨论一个8*8的分块,先把前8*4中的4*4先转置,然后再把后4*4挪到转置
                //块里的前8*4的后4*4分块中
                for(x=i;x<i+4;x++){
                 //x1-x4负责正常的转置即前四行前四列
                    //x5-x8负责前四行后四列的提前转置
                    x1=A[x][j],x2=A[x][j+1],x3=A[x][j+2],x4=A[x][j+3];
                    x5=A[x][j+4],x6=A[x][j+5],x7=A[x][j+6],x8=A[x][j+7];
                    B[j][x]=x1,B[j+1][x]=x2,B[j+2][x]=x3,B[j+3][x]=x4;
                    B[j][x+4]=x5,B[j+1][x+4]=x6,B[j+2][x+4]=x7,B[j+3][x+4]=x8;
                    
                }
                //把后四行前四列转置,同时把提前转置的平移过去
                for(y=j;y<j+4;y++){
                    x1=A[i+4][y],x2=A[i+5][y],x3=A[i+6][y],x4=A[i+7][y];
                    x5=B[y][i+4],x6=B[y][i+5],x7=B[y][i+6],x8=B[y][i+7];

                    B[y][i+4]=x1,B[y][i+5]=x2,B[y][i+6]=x3,B[y][i+7]=x4;
                    //把存在B中的右上角的数字往左下角挪,注意偏移量
                    B[y+4][i]=x5,B[y+4][i+1]=x6,B[y+4][i+2]=x7,B[y+4][i+3]=x8;
                }
                //最后面的常规转置
                for(x=i+4;x<i+8;x++)
                {
                    x1=A[x][j+4],x2=A[x][j+5],x3=A[x][j+6],x4=A[x][j+7];
                    B[j+4][x]=x1,B[j+5][x]=x2,B[j+6][x]=x3,B[j+7][x]=x4;
                }
            }
        }
}

得到的miss数量为

1	hits:9066, misses:1179, evictions:1147

最优解法

最优解法逼近理论最优1024,这是别人写的,我没尝试,累了.

Phase_3:61*67

尝试不同的分块方式

4*4(以此为例子,在这种方式下测试出不同分块情况下的miss数量,枚举)

char trans_7_desc[]="对于61*67在这里尝试各种各样的分块4*4";
void trans_7(int M, int N, int A[N][M], int B[M][N]){
    int i,j,x,y;
    for(i=0;i<N;i+=4)
    for(j=0;j<M;j+=4){
        for(x=i;x<i+4&&x<N;x++){
            for(y=j;y<j+4&&y<M;y++)
            B[y][x]=A[x][y];
        }
    }
}

miss数量:

分块规模	Miss数量
4×4	2425
8×8	2118
14×14	1996
15×15	2021
16×16	1992
17×17	1950
18×18	1961
19×19	1979
20×20	2002
21×21	1957

61 × 67: 10 points if m < 2, 000, 0 points if m > 3, 000

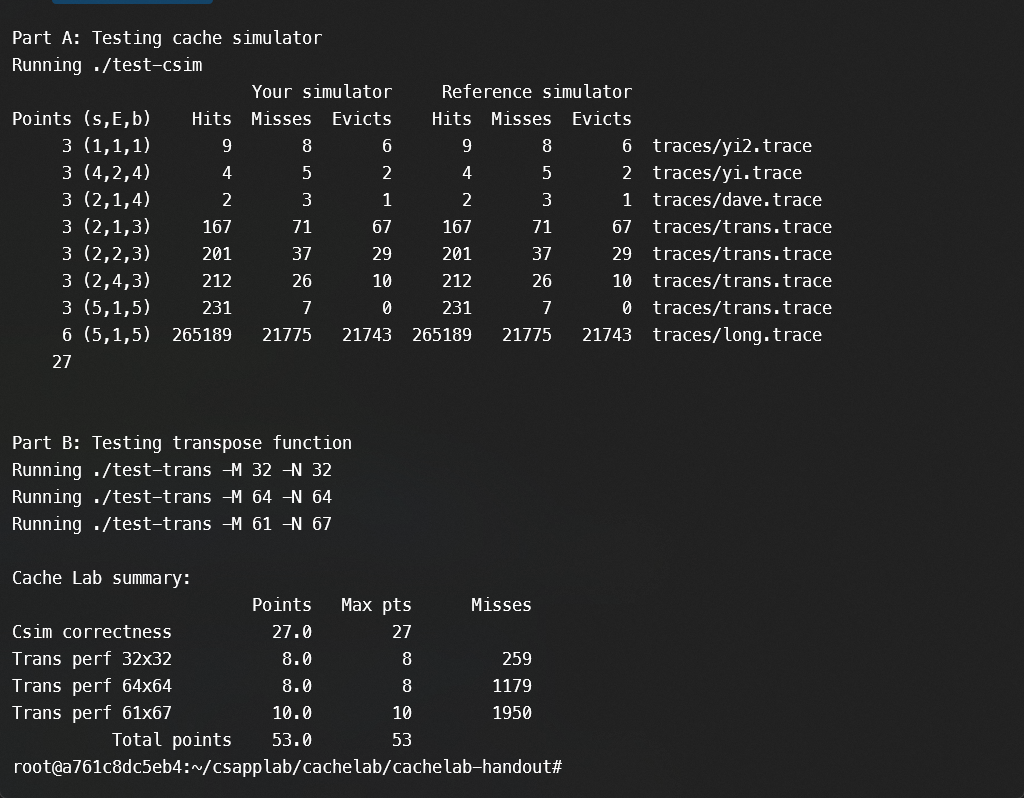
所以我们选择17*17分块上交答案,用几个if else 函数编辑submission函数,使用.driver.py脚本运行测试分数就此通关,

如图:

完美收官,并且miss数尽量达到最小!

Lab小结

Part_1

这次的lab真的是比之前的难太多了,part_1还是好的,偷偷看了看别人的参考答案就码出来了,分情况讨论下几种miss,hit,eviction,主要能学习到以下几个函数的用法,分别是

getopt
fscanf
malloc
fopen

第一次体会到如何从大量数据中快速读取所需要的信息,也才知道原来main函数是有默认参数的,并且默认参数是这样的意思int argc char ** argv,确实有意思,美中不足的是这个lab不用考虑Block太小了导致存放数据要横跨两个Block的这种情况(可能有这种情况吧?)所以我们不用考虑B的大小对miss与否的影响,降低了部分难度

Part_2

Part_2确实是把我恶心坏了,坏透了的那种,从4*4开始就开始困惑,大脑在这几天一直在模拟cache的运行,各种冲突对撞,又因为有好多不知道的,网上的解析也没有说明的小东西,故而越发困惑,当然也在不断的实操中了解加深了Cache的运行(超简单版本),明白了其基本理念,虽然啊,鼠鼠我还是没有写作业(csapp课本上的),也没有看课本,只是听完了教授的课程,对着ppt和pdf和网上的一大堆教程开始硬抗着这恶心的lab.

不管之后会忘记多少,现在先做了再说,再把这教程敲完,把自己不会的全部补上,供后来人学习.便是鼠鼠我的价值.

CSAPP的lab5-cachelab